Star Formation with Radiative TransferMatthew R. Bate These calculations take my star cluster calculations to a new level of complexity, modelling the collapse and fragmentation of 50 solar mass clouds but including radiative feedback from the young protostars. The initial conditions were identical to those in the original calculation and the second hydrodynamical calculation that I performed. Radiative feedback dramatically reduces the number of objects formed and results in a higher ratio of stars to brown dwarfs. Refereed Scientific Papers
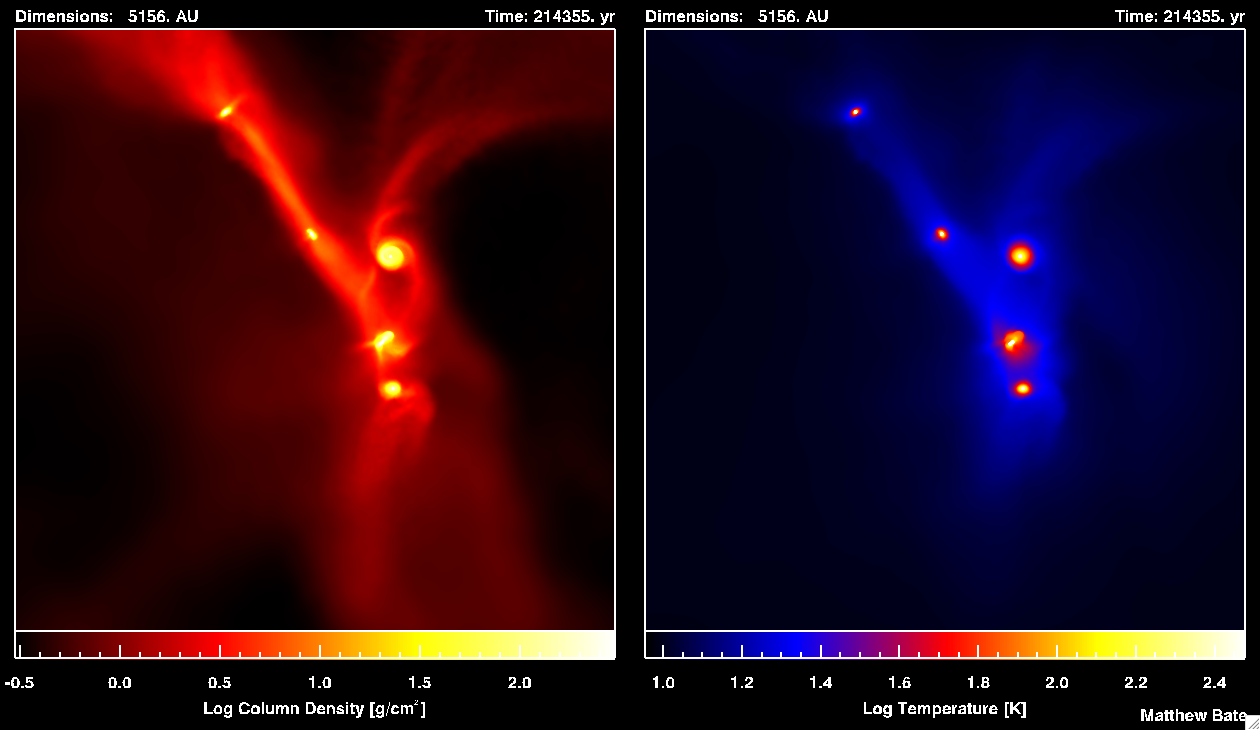
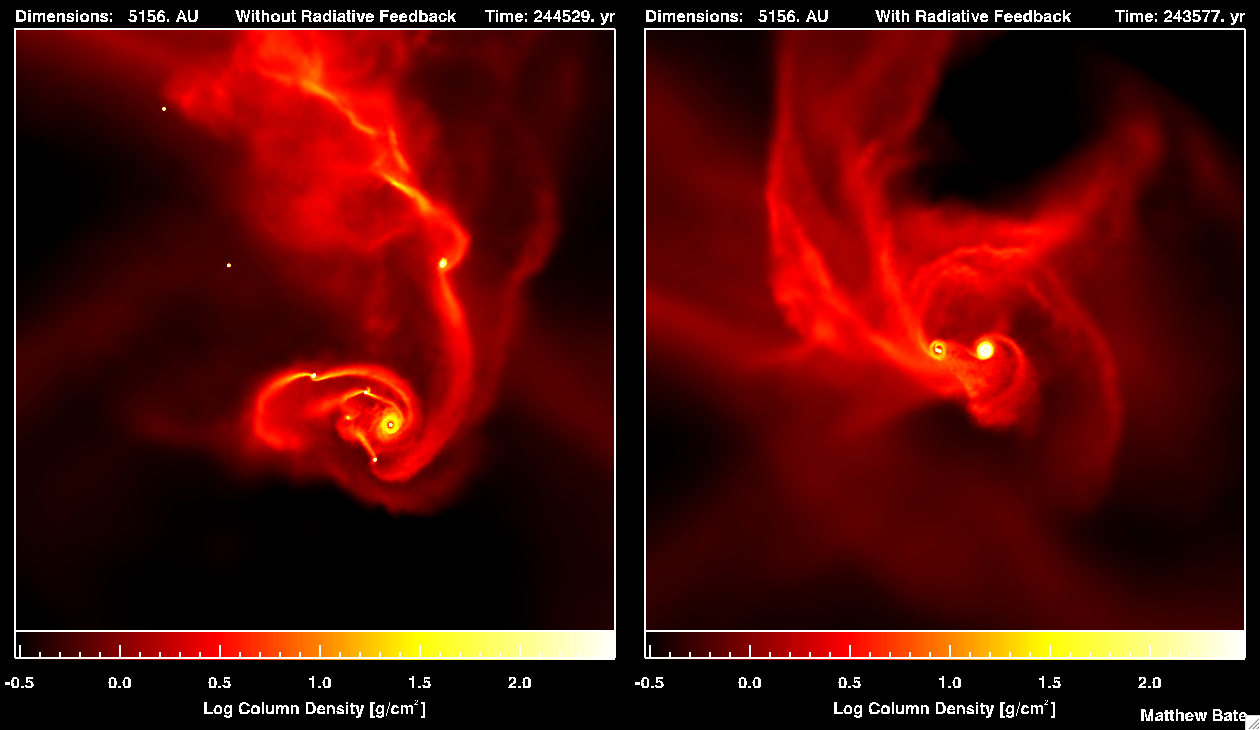
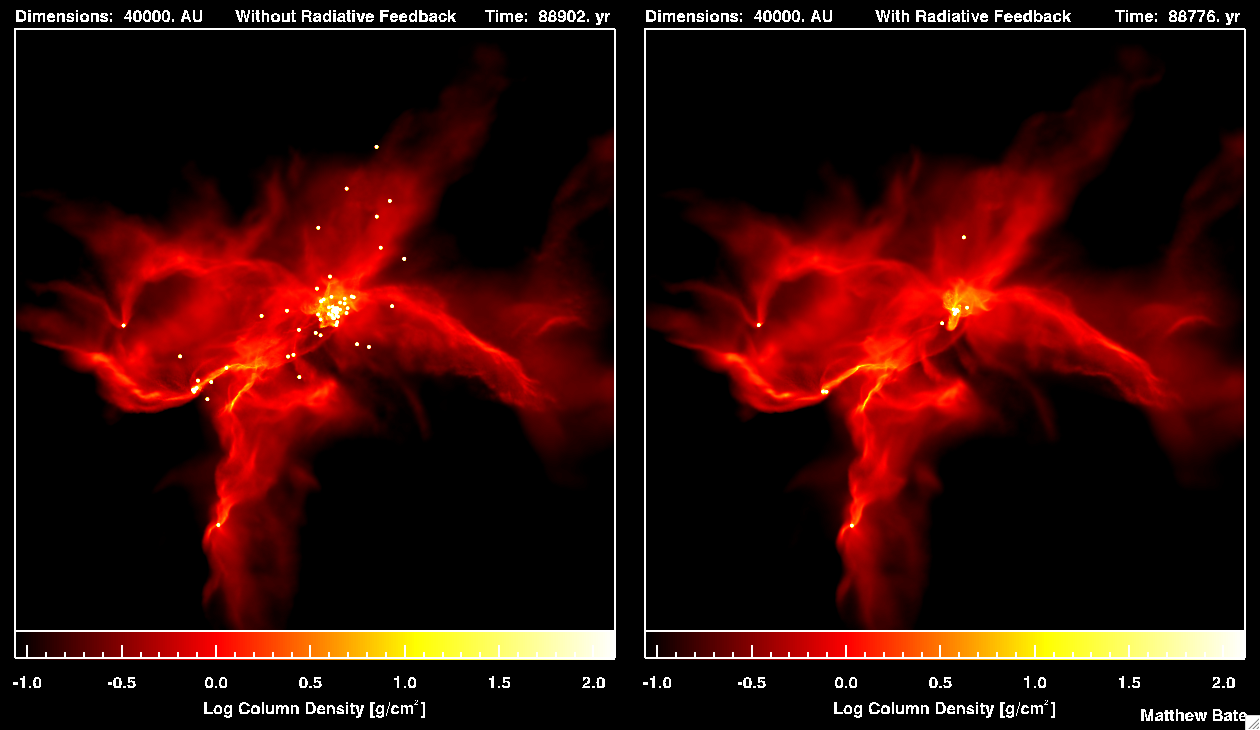
"The importance of radiative feedback for the stellar initial mass function" AnimationsSimulation & visualisation by Matthew Bate, University of Exeter unless stated otherwise. There are four movies, two for each of the two calculations. In each case, the first movie shows the gas density and temperature evolution for the radiation hydrodynamical calculation. The second movie in each case compares the evolution of the density without and with radiative feedback (i.e. compares the earlier hydrodynamical simulation with the radiation hydrodynamical simulation). A movie from 2005 also compares the density evolution of the original two hydrodynamical calculations. The animations below both use my typical red-yellow-white colour scheme to visualise the column density through the star-forming cloud (left) and my blue-red-yellow-white colour scheme (right) to visualise temperature (actually mass-weighted temperature integrated through the cloud). Calculation 1: re-run of the original star cluster formation simulation
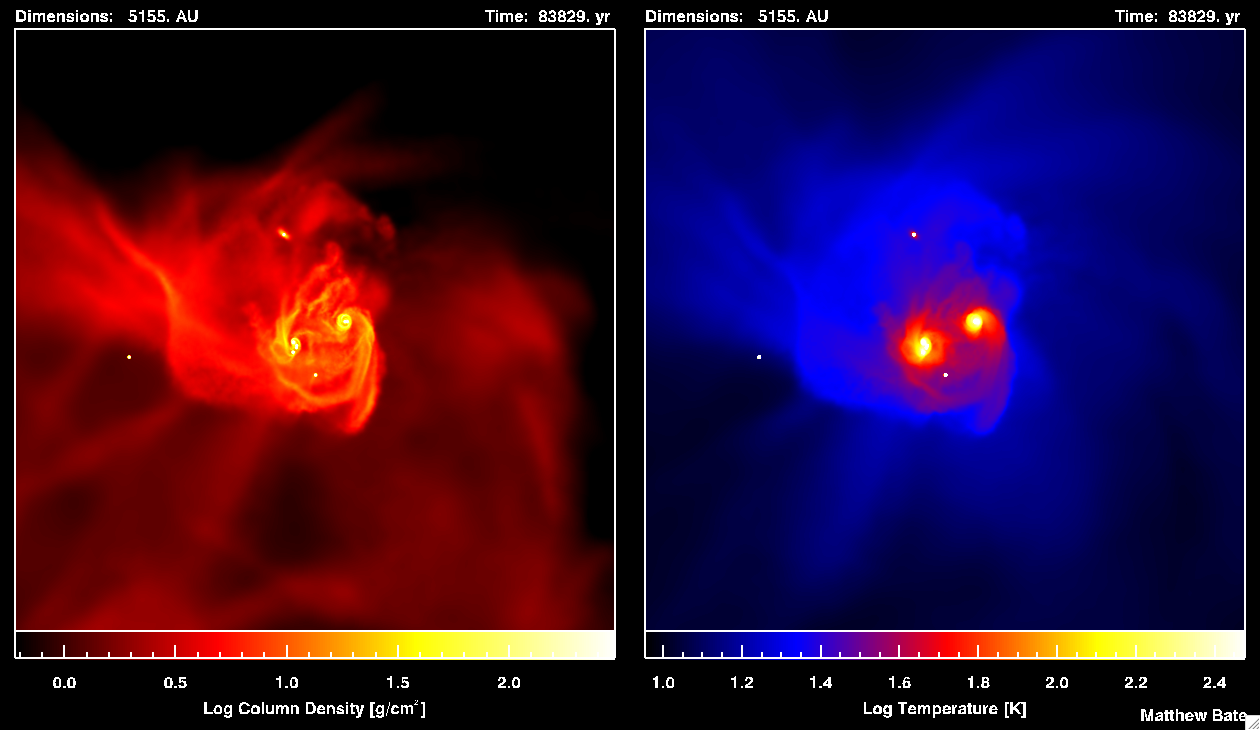
Calculation 2: re-run of the second calculation that begins with a denser cloud
Copyright: The material on this page is the property of Matthew Bate. Any of my pictures and animations may be used freely for non-profit purposes (such as during scientific talks) as long as appropriate credit is given wherever they appear. Permission must be obtained from me before using them for any other purpose (e.g. pictures for publication in books).
Notes on formats: Technical DetailsThe calculations model the collapse and fragmentation of 50 solar mass molecular clouds that are 0.375 pc or 0.180 pc in diameter (approximately 1.2 and 0.6 light-years, respectively). At the initial temperature of 10 K with a mean molecular weight of 2.38, this results in an thermal Jeans mass of 1 solar mass. The free-fall time of the first type of cloud is 190,000 years and the simulations cover 266,000 years. The free-fall time of the denser cloud is 63,400 years and the simulations cover 89,000 years. The clouds are given an initial supersonic `turbulent' velocity fields in the same manner as Ostriker, Stone & Gammie (2001). We generate a divergence-free random Gaussian velocity field with a power spectrum P(k) \propto k-4, where k is the wave-number. In three-dimensions, this results in a velocity dispersion that varies with distance, lambda, as sigma(lambda) \propto lambda1/2 in agreement with the observed Larson scaling relations for molecular clouds (Larson 1981). This power spectrum is slighly steeper than the Kolmogorov spectrum, P(k)\propto k11/3. Rather, it matches the amplitude scaling of Burgers supersonic turbulence associated with an ensemble of shocks (but differs from Burgers turbulence in that the initial phases are uncorrelated). The two calculations use the same initial velocity field. The calculations were performed using a parallel three-dimensional smoothed particle hydrodynamics (SPH) code with 3.5 million particles on the United Kingdom Astrophysical Fluids Facility (UKAFF) and the University of Exeter Supercomputer. They each took approximately 40000 CPU hours running on 8 to 16 processors. The SPH code was parallelised using OpenMP by M. Bate. The code uses sink particles (Bate, Bonnell & Price 1995) to model condensed objects (i.e. the stars and brown dwarfs). Sink particles are point masses that accrete bound gas that comes within a specified radius of them. This accretion radius is to set 0.5 AU. Thus, the calculation resolves circumstellar discs with radii down to approximately 1 AU. High Resolution Still Images and Commentary
Not yet available.
| ||||||||||||||||||