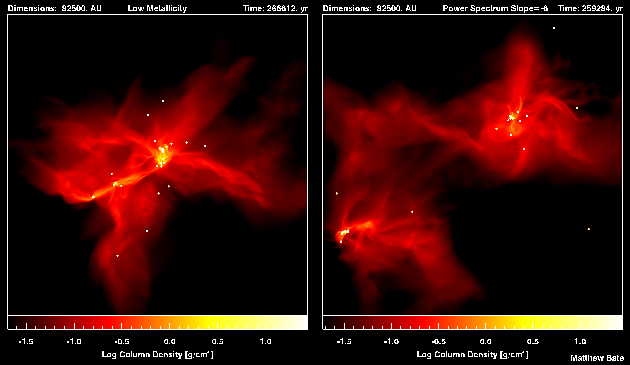
The Dependence of the Initial Mass Function on Metallicity, and the Opacity Limit for FragmentationMatthew R. Bate This was the third large-scale calculation to be performed. The initial conditions were identical to those in the original calculation. However, the equation of state was modified to mimic the thermal behaviour of low metallicity gas. In practice, the gas collapsed isothermally until a density of 1.1x10-14 g cm-3, after which it began to heat up. In the original calculation, the heating began at a density nine times greater (i.e. 1.0x10-13 g cm-3). The effect of this is to increase the minimum mass of a fragment by a factor of three from approximately 3 Jupiter masses to approximately 9 Jupiter masses. Refereed Scientific Papers
"The Dependence of the Initial Mass Function on Metallicity, and the Opacity Limit for Fragmentation" AnimationsCopyright: The material on this page is the property of Matthew Bate. Any of my pictures and animations may be used freely for non-profit purposes (such as during scientific talks) as long as appropriate credit is given wherever they appear. Permission must be obtained from me before using them for any other purpose (e.g. pictures for publication in books). Simulation & visualisation by Matthew Bate, University of Exeter unless stated otherwise.
Notes on formats:
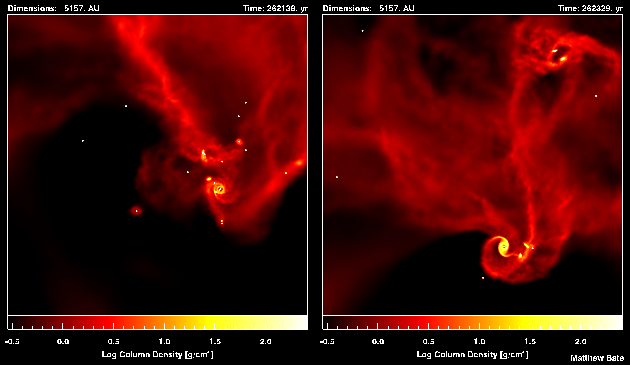
Technical DetailsThe calculation models the collapse and fragmentation of a 50 solar mass molecular cloud that is 0.375 pc in diameter (approximately 1.2 light-years). At the initial temperature of 10 K with a mean molecular weight of 2.46, this results in an thermal Jeans mass of 1 solar mass. The free-fall time of the cloud is 190,000 years and the simulation covers 266,000 years. The cloud is given an initial supersonic `turbulent' velocity field in the same manner as Ostriker, Stone & Gammie (2001). We generate a divergence-free random Gaussian velocity field with a power spectrum P(k) \propto k-4, where k is the wave-number. In three-dimensions, this results in a velocity dispersion that varies with distance, lambda, as sigma(lambda) \propto lambda1/2 in agreement with the observed Larson scaling relations for molecular clouds (Larson 1981). This power spectrum is slighly steeper than the Kolmogorov spectrum, P(k)\propto k11/3. Rather, it matches the amplitude scaling of Burgers supersonic turbulence associated with an ensemble of shocks (but differs from Burgers turbulence in that the initial phases are uncorrelated). The calculation was performed using a parallel three-dimensional smoothed particle hydrodynamics (SPH) code with 3.5 million particles on the United Kingdom Astrophysical Fluids Facility (UKAFF). It took approximately 75000 CPU hours running on up to 64 processors. The SPH code was parallelised using OpenMP by M. Bate. The code uses sink particles (Bate, Bonnell & Price 1995) to model condensed objects (i.e. the stars and brown dwarfs). Sink particles are point masses that accrete bound gas that comes within a specified radius of them. This accretion radius is to set 5 AU. Thus, the calculation resolves circumstellar discs with radii down to approximately 10 AU. Binary systems are followed to separations as small as 1 AU. Copyright: Matthew Bate, University of Exeter.
| |||||||||