The Statistical Properties of Stars and Their Dependence on Metallicity: the Effects of OpacityMatthew R. Bate We report the statistical properties of stars and brown dwarfs obtained from four radiation hydrodynamical simulations of star cluster formation that resolve masses down to the opacity limit for fragmentation. The calculations are identical except for their dust and gas opacities. Assuming dust opacity is proportional to metallicity, the calculations span a range of metallicities from 1/100 to 3 times solar, although we emphasise that changing the metallicity has other thermodynamic effects that the calculations do not capture (e.g. on the thermal coupling between gas and dust). All four calculations produce stellar populations whose statistical properties are difficult to distinguish from observed stellar systems, and we find no significant dependence of stellar properties on opacity. The mass functions and properties of multiple stellar systems are consistent with each other. However, we find protostellar mergers are more common with lower opacities. Combining the results from the three calculations with the highest opacities, we obtain a stellar population consisting of more than 500 stars and brown dwarfs. Many of the statistical properties of this population are in good agreement with those observed in our Galaxy, implying that gravity, hydrodynamics, and radiative feedback may be the primary ingredients for determining the statistical properties of low-mass stars. However, we do find indications that the calculations may be slightly too dissipative. Although further calculations will be required to understand all of the effects of metallicity on stellar properties, we conclude that stellar properties are surprisingly resilient to variations of the dust and gas opacities. Refereed Scientific Papers
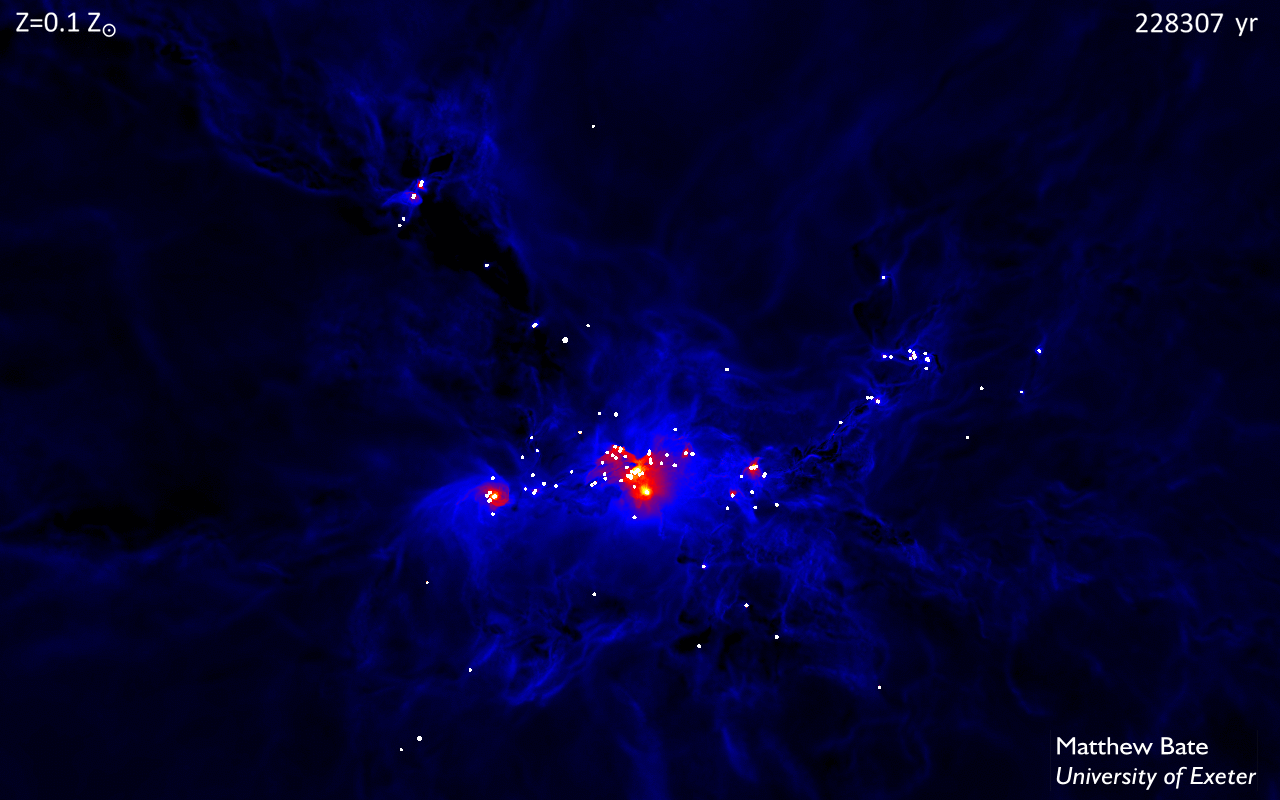
"The statistical properties of stars and their dependence on metallicity" AnimationsSimulation & visualisation by Matthew Bate. For each of the four calculations, there are two versions of the movie. One uses my typical red-yellow-white colour scheme to visualise the column density through the star-forming cloud. The other uses a black-blue-red-yellow-white colour scheme to visualise the temperature (mass weighted) through the star-forming cloud. On large scales, few differences are apparent in the column density animations, but the temperature movies differ substantially from one another. Click on the images to view the animations (in Quicktime format).
Copyright: The material on this page is the property of Matthew Bate. Movies and images are released under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 License. Technical DetailsThe calculations model the collapse and fragmentation of 500 solar mass molecular clouds that are 0.8 pc in diameter (approximately 2.6 light-years). At the initial temperature of 10 K with a mean molecular weight of 2.38, this results in an thermal Jeans mass of 1 solar mass. The free-fall time of the cloud is 190,000 years and the simulations cover 228,000 years. The clouds are given an initial supersonic `turbulent' velocity field in the same manner as Ostriker, Stone & Gammie (2001). We generate a divergence-free random Gaussian velocity field with a power spectrum P(k) \propto k-4, where k is the wave-number. In three-dimensions, this results in a velocity dispersion that varies with distance, lambda, as sigma(lambda) \propto lambda1/2 in agreement with the observed Larson scaling relations for molecular clouds (Larson 1981). This power spectrum is slighly steeper than the Kolmogorov spectrum, P(k)\propto k11/3. Rather, it matches the amplitude scaling of Burgers supersonic turbulence associated with an ensemble of shocks (but differs from Burgers turbulence in that the initial phases are uncorrelated). The calculations were performed using a parallel three-dimensional smoothed particle hydrodynamics (SPH) code with 35 million particles on the University of Exeter Supercomputer. Each of the non-solar metallicity calculations took 0.7 - 1 million core-hours running on 96 compute cores (8 compute nodes). The SPH code was parallelised using both MPI and OpenMP by M. Bate. The code uses sink particles (Bate, Bonnell & Price 1995) to model condensed objects (i.e. the stars and brown dwarfs). Sink particles are point masses that accrete bound gas that comes within a specified radius of them. This accretion radius is to set 0.5 AU. Binary systems are followed to separations as small as 0.015 AU - closer systems are assumed to merge. Four calculations were performed which were identical to each other except for the dust and gas opacities used when modelling the radiative transfer. The opacities used were those appropriate for molecular clouds with metallicities of 1/100, 1/10, 1, and 3 times solar metallicity. However, it is important to note that in reality, changing the metallicity has other thermodynamic effects that the calculations do not capture. In particular, the calculations assume that gas and dust are well coupled thermally, an approximation that quickly breaks down either at low metallicities or low densities. Further calculations will be required to understand all of the effects of metallicity on stellar properties. Copyright: Matthew Bate, University of Exeter.
|