Circumstellar Disks with Planets

Introduction

Over the past few years, considerable efforts have been made to examine the gravitational perturbations induced in a circumstellar disk by an orbiting planetary mass body. Gravitational interactions between the planet and the surrounding material lead to an exchange of angular momentum. As a result, both the morphology of the disk and the orbital elements of the planet are affected.
The most prominent features arising in a disk containing a planet are a low-density annular region along the planet's path (known as gap) and spiral wave patterns, emanating from the Lagrangian points. The extent to which the disk is marked by such signatures depends on the mass of the perturbing body as well as on the viscosity of the circumstellar medium.
The importance of the peculiar appearance of circumstellar disks hosting planets lies in the possibility that it may be exploited for identifying and observing planets still in the formation process.

The results presented here have been obtained by performing two-dimensional thermo-hydrodynamical simulations of circumstellar disks with embedded planets of different masses. Furthermore, various viscosity regimes have been considered. In order to investigate separately what kind of bearing these physical properties has on the disk morphology, two comparisons are shown:
  1. Disks with different viscosities
  2. Planets with different masses


Disks with Different Viscosities

Simulations of a Jupiter mass (MJ) protoplanet embedded in disk models with kinematic viscosity ν=1015, 5×1015, and 1016 cm2 s-1 have been carried out. Viscosity acts to smooth out all dishomogeneities, and therefore it tends to suppress the formation of the gap. The main outcomes of this comparison are:
  • Only when the viscosity is small enough a deep and wide gap is carved in by the planet, otherwise it reduces to a shallow trough.
  • The gap feature is a property affecting not only the density distribution but also the distribution of pressure, temperature, optical thickness, and radiated flux.
  • Average temperatures inside the gap can be rather cold and even lower than 20 K.
  • The relative disk thickness H/r is on the order of 0.04 and its shape is such to shade the planet against the stellar radiation.
Some of these points are illustrated in the images and the graphs presented below.

Surface Density Midplane Temperature
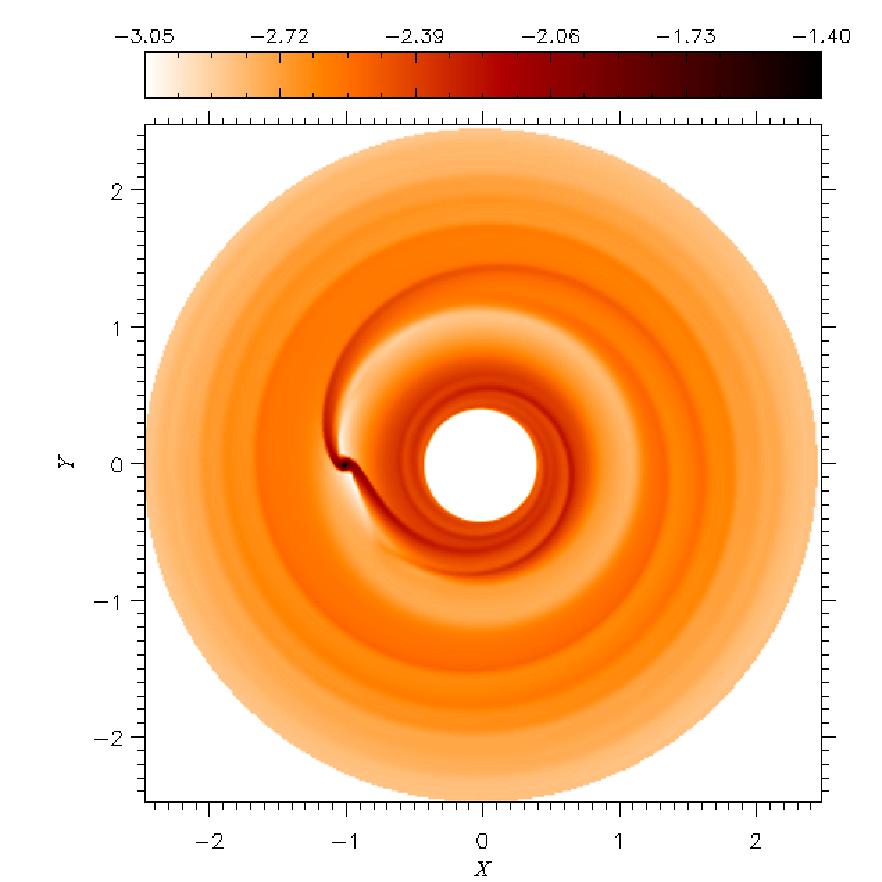Surface Density: High Viscosity Midplane Temperature: High Viscosity
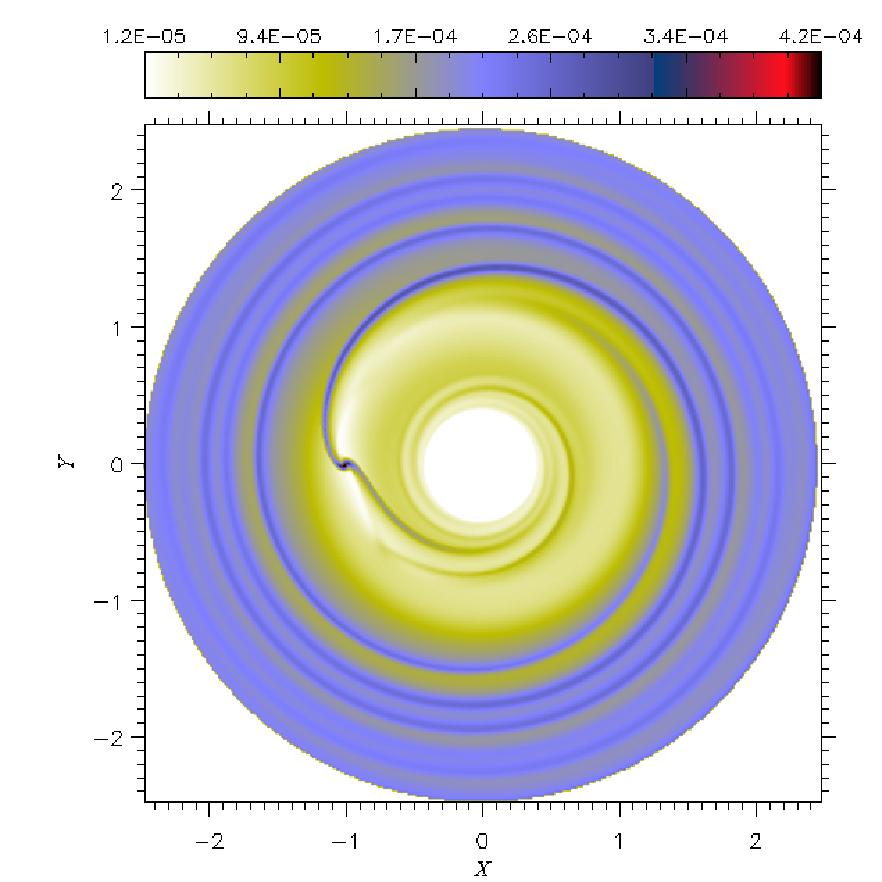
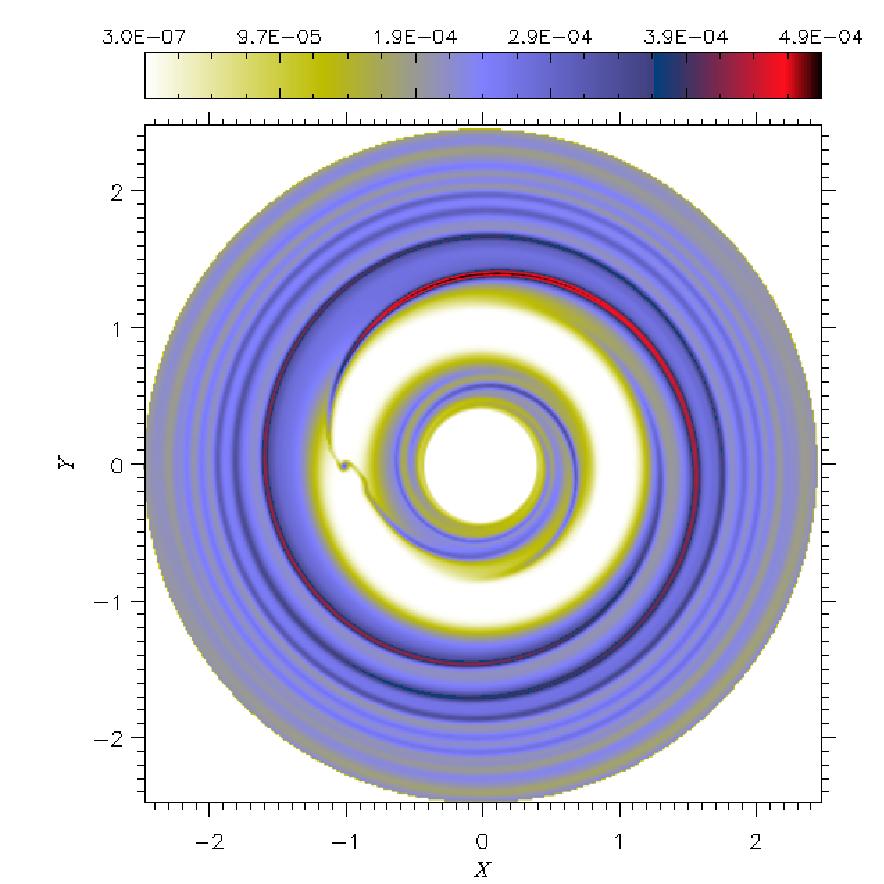
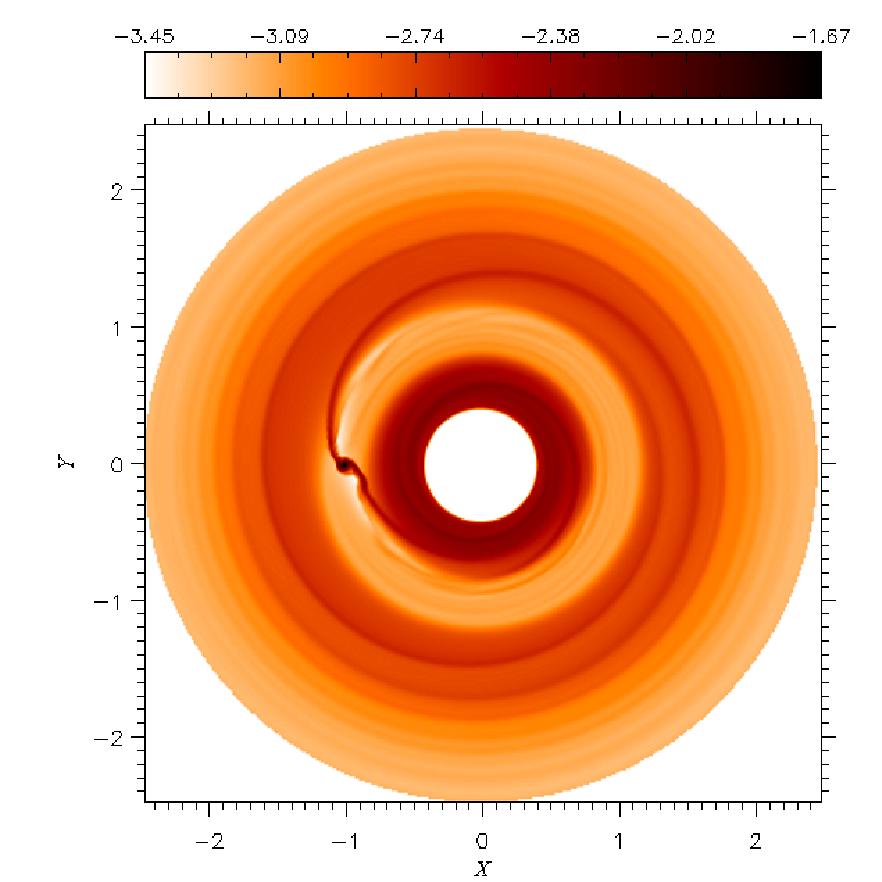
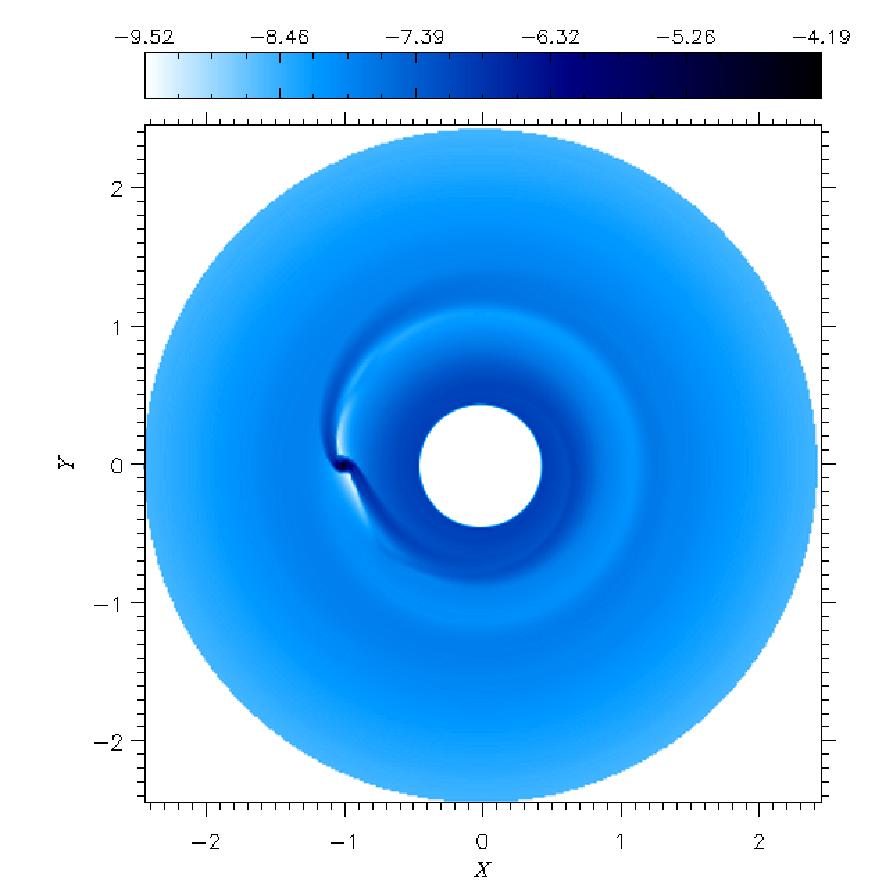
The images above show the surface density (left) and the midplane temperature (right) of a disk with ν=1016 cm2 s-1. The images below refer to the same quantities within a disk with ν=1015cm2 s-1. Temperature distribution is in log-scale. The planet is located at (X,Y)=(-1,0). In color-bar units, 10-4corresponds to 33 g cm-2 and 10-2 equals 198 K. [Click on the images to enlarge].
Surface Density: Low Viscosity Midplane Temperature: Low Viscosity

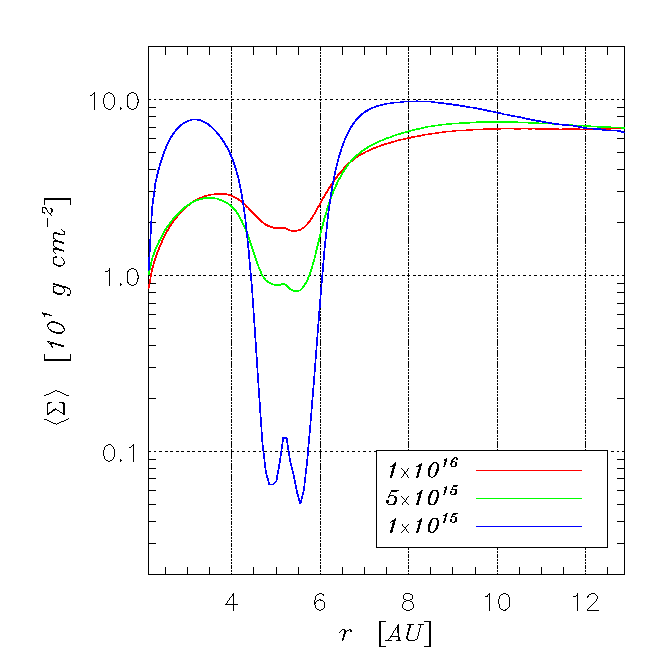
Average Surface Density Average Midplane Temperature
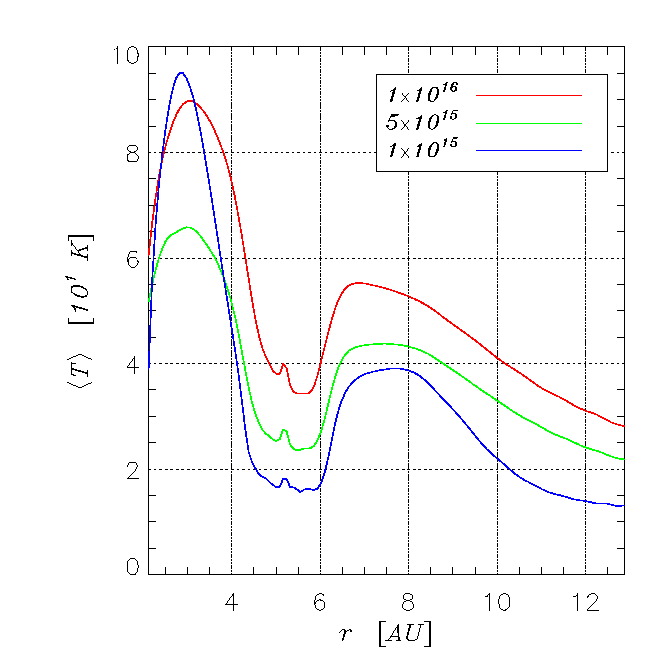Surface Density Profiles Midplane Temperature Profiles
The above plots show the azimuthally averaged surface density (left) and the midplane temperature (right) of disks with different kinematic viscosities (values quoted in the legend are in cgs units). As viscosity becomes larger, viscous torques grow stronger and more efficient in opposing gravitational torques. Hence, the gap is partially filled in.

Average Disk Thickness
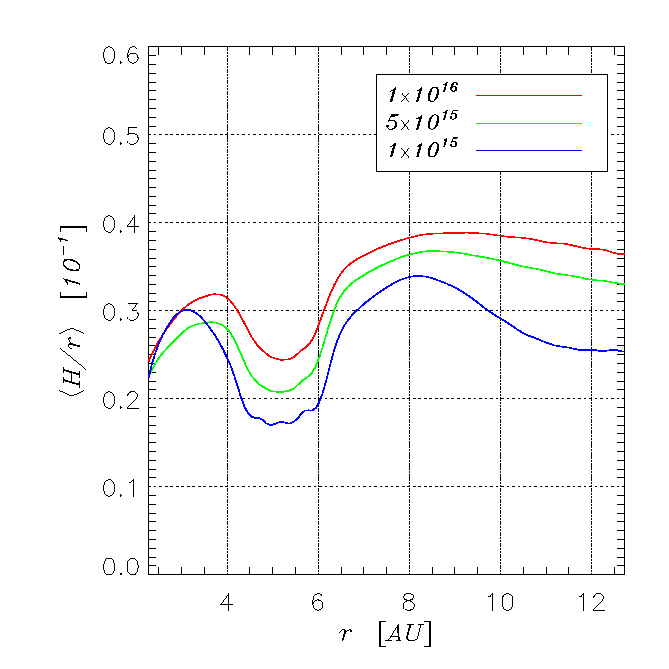Aspect Ratio Profiles The plot indicates how the azimuthally averaged aspect ratio of a disk (i.e., H/r) varies according to the magnitude of the kinematic viscosity (see legend). The trough at the planet location is generated by the temperature gap combined with the gravitational field of the planet. As a result of this disk thickness profile, the planet can be shaded against direct radiation from the central star. [Click on the image to enlarge].

Emitted Flux
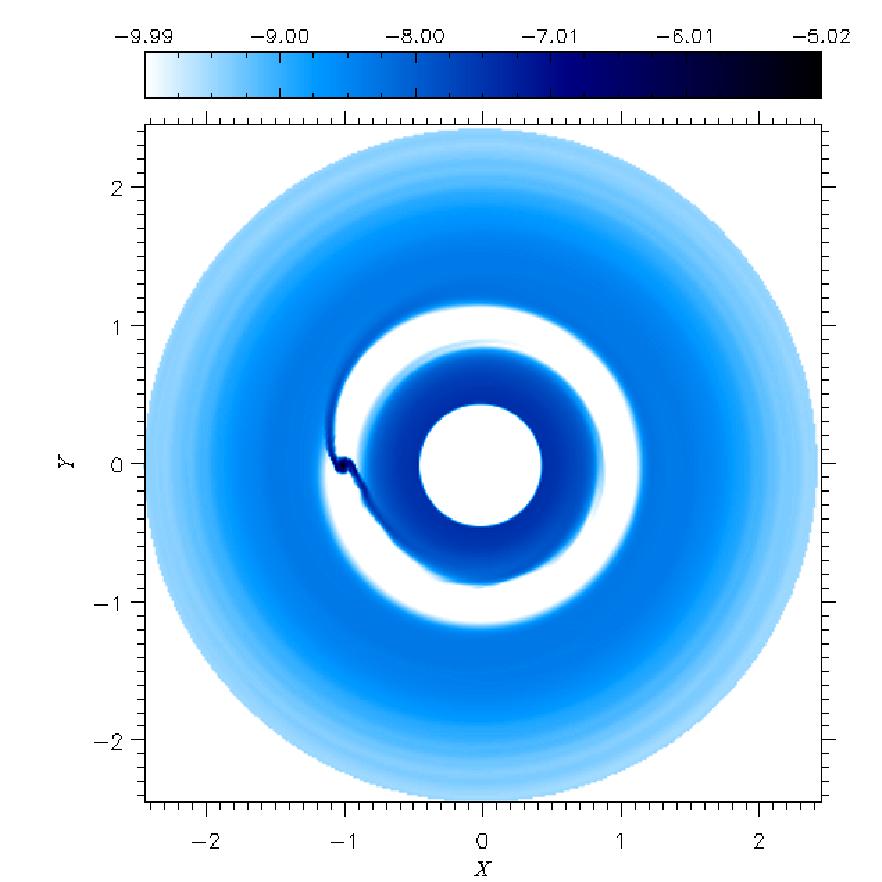Emitted Flux: High Viscosity Emitted Flux: High Viscosity
This above are the fluxes emitted by a disk with viscosity ν=1016 cm2 s-1 (left) and with ν=1015 cm2 s-1 (right). In the plot units, 10-5 corresponds to 4.7×104 erg cm-2 s-1, which is six orders of magnitude smaller than the surface flux of the Sun. [Click on the images to enlarge].


Planets with Different Masses

Along with the investigation of effects due to viscosity, the impact of the planetary mass on the disk morphology has been also examined by performing computations of 0.1, 0.2, and 0.5 MJ objects. The ability of a planet to dig a gap greatly reduces when its mass is smaller than roughly 0.2 MJ (66 Earth masses), especially if it dwells in a high viscosity environment. This is quantitatively shown below.

Surface Density Midplane Temperature
Surface Density: High Viscosity Midplane Temperature: High Viscosity
These images illustrate the surface density (left) and the midplane temperature (right) of a disk with ν=1015 cm2 s-1 with an embedded planet of 0.1 Jupiter masses. Temperature is in log-scale. As before, in color-bar units, 10-4 corresponds to 33 g cm-2 and 10-2 equals 198 K. [Click on the images to enlarge].

Average Surface Density Average Midplane Temperature
Surface Density Profiles Midplane Temperature Profiles
The plots above show the azimuthally averaged surface density (left) and the midplane temperature (right) of disks containing planetary objects of different mass: 0.5 MJ (solid line), 0.2 MJ (short-dash line), and 0.1 MJ (long-dash line). Both the density and the temperature gap get shallower as the planet's mass gets smaller. This happens because gravitational torques exerted by the planet are not able to sustain viscous torques. [Click on the images to enlarge].

Disk Thickness
Aspect Ratio around a Low Mass Planet Even when the embedded body is not very massive, its gravitational potential induces the formation of a cavity that hides the planet from stellar irradiation. In the case reported here, the planet has a mass of 0.1 MJ and resides in a disk with viscosity ν=1016cm2 s-1. [Click on the image to enlarge].

Emitted Flux
Emitted Flux: Low Mass Planet This is the map of the energy flux radiated by a disk having a viscosity ν=1015 cm2 s-1 and harbouring a 0.1 MJ planet. Although the magnitude of the viscosity is rather small, the planet has not a significant impact on the background disk emission. [Click on the image to enlarge].

Return to my homepage